■続々ACIIアートの秘密 
階調変換 その2
前々回の
の時にASCIIアートに関する情報を探した- 清竹's テキスト絵 HPリンク集 (http://www2.nkansai.ne.jp/users/kiyo/ )
「限られた出力階調を有効に利用するため、画像の濃度ヒストグラムの補正を行ないます。1パス目で、濃度ヒストグラムをカウントし、そこからヒストグラムが平坦になるような濃度変換関数を生成します。(ヒストグラムを平坦にするのは、情報のエントロピーをなるべく保存するためです。)」とある。Q02TEXTはimage2asciiと同様のテキストアート作成プログラムである。前回のの最後で(3).情報量を最大にするモデル というのを導入したが、これがそのエントロピー最大化アルゴリズムに近いものを導入してみたものである。何しろ、この考えを使っていくのは乏しい階調性の出力機器には非常に有効なのだ。今回は、この「エントロピー最大化アルゴリズム」について考えてみたい。
Q02TEXTは「 .:|/(%YVO8D@0#$」の16階調を使用するテキストアート作成プログラムである。それに対して、「ASCIIアートの秘密」で作成したimage2asciiが使用可能な階調数は一定ではない。指定されたフォントを一旦出力してみて、その結果を計測することにより、出力可能な階調数を決定している。したがって、指定したフォントでしか階調の確かさは保証されない。その代わりに、指定されたフォントを使えば割に豊かな階調性を使用できることになる。
また、得られる階調は一般的に滑らかではないので、Q02TEXTが使っているアルゴリズムとは少し違うものを導入している。
通常ASCIIアートは色々な環境で見ることができるのがメリットの一つである。しかし、image2asciiはフォントを限定してしまっている。これは、目的が通常のASCIIアートとは異なるからである。私がimage2asciiを作った目的は、それを仮想的な出力デバイスとしてみたいからである。その出力で生じる様々な問題を調べたり、解決してみたいのである。
さて、前回の最後に示した3種類の画像変換は
- 単純な階調重視モデル
- オリジナルの0を出力画像の最小値に
- オリジナルの255を出力画像の最大値にする
- 拡大した単純な階調重視モデル
- オリジナルの最小値を出力画像の最小値に
- オリジナルの最大値を出力画像の最大値にする
- 情報量を最大にするモデル
- エントロピーを最大にするための階調変換を行う
これら3つの変換方法の違いにより出力画像にどのような違いが生じていたかを、まずはもう一度見てみる。まずは、オリジナル画像である。これは、「私の尊敬する」S大先生である。私は尊敬とともに「ロボコップSさん」あるいは、「ロボSさん」と呼ぶのだ。いや、本当に。
 |
以下にオリジナル画像及びimage2asciiを用いて変換したものを示す。
 |  |  |  |
- (1).単純な階調重視モデルが比較的白い個所では一番オリジナルに忠実な濃度であることはわかるだろう。ただし、黒い部分に関しての表現力は極めて低い。
- (2).階調性を少しだけ改善したものではそれより視認性が改善している。
- (3).視認度の高い画像ではあるが、オリジナルとは濃度などは異なる?
それでは、これらの画像のヒストグラムを調べてみる。先の「(ヒストグラムを平坦にするのは、情報のエントロピーをなるべく保存するためです。)」というのとの関係を調べたいわけである。
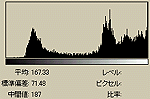 |  | 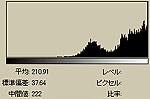 | 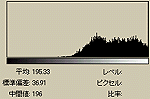 |
ASCII ARTには濃度の表現領域には限度がある。そのため、(1),(2),(3)はいずれも濃度が最大を示す個所でもオリジナルよりかなり濃度が低い。また、(1),(2)はオリジナルとヒストグラムの形状も少しは「似ている」が、(3)においては、かなり異なっているのがわかると思う。(3)はヒストグラムの形状はかなり異なるにも関わらず、視認度は高くなっている。これが、エントロピーを最大化(すなわち情報量を最大化)しているおかげである。ヒストグラムがかなり平坦になっているのがわかるだろう。
というならば、エントロピーの計算もしなければならないだろう。もちろんエントロピーと言えば、
でも登場している。「エントロピーは増大するのみ...」というフレーズで有名なアレである。情報量を示す値だといっても良いだろう。せっかく、「ハードディスク...」の回で計算をしたのだから、今回もその計算を流用してエントロピーを計算してみたい。といっても、無記憶情報源(Zero-memorySource)モデルに基づけば、ヒストグラムが平坦すなわち各濃度の出現確率が等確率に近いほどエントロピーは高いのが当たり前であるが... この前作成したMathematicaのNotebookを流用するために、オリジナルと3つの変換画像を合体させる。そして、そのヒストグラムを見てみよう。このヒストグラムが非常にわかりにくいと思うので、一応説明しておく。あるY軸の値で水平に1ライン抽出して、その部分のヒストグラムを右のグラフに示しているのである。
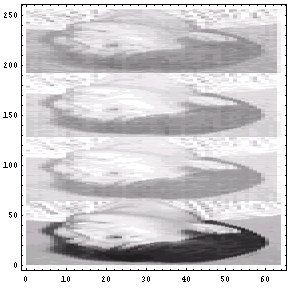 | 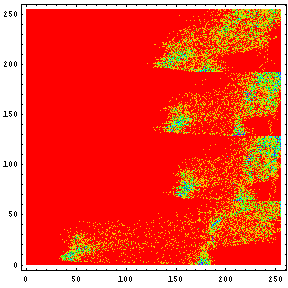 |
例えば、オリジナルの画像では髪の毛がある辺り(Y軸で10から30位)では、ヒストグラムを見ればレベルが50位の黒い所が多いところがわかる。それに対して、変換後の画像では、一番濃度の高い所でも150前後であることがわかるだろう。
それでは、それぞれ、Y軸でスライスしてその断面におけるエントロピーを計算したものを次に示してみる。
 | 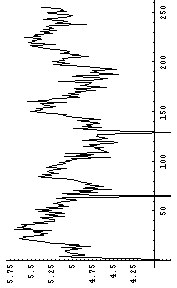 |
本来は、画像全面におけるエントロピーを計算するのが、望ましい。しかし、ここで使っているような、Y軸でスライスしてその断面におけるエントロピーでも、オリジナルの画像が一番エントロピーが高く、(3)の変換画像(つまり一番上)のものが次にエントロピーが高いのがわかると思う。つまり、情報量が高いのである。
エントロピー量とあなたの感じる「視認度」とが相関があるかどうかは非常に興味があるところだ(私にとって)。エントロピーが多くても(すなわち情報量が多くても)オレはちっともいいと思わないよ、とか、おれは断然エントロピー派だね、とか色々な意見があったらぜひ私まで教えてほしい。
「お遊び」に見えるASCIIアートも、調べていくと実は奥が深いのだなぁ、とつくづく思う。といっても、もちろん本WEBはお遊びである。なかなか、奥までは辿りつかない(し、辿りつけない)と思うが、この「ASCIIアートの秘密」シリーズはまだまだ続くのである。