hirax.net::inside out::05月12日

■体調が悪くなるわけだ　

　起きると朝から体調が悪いが、東京へ。用事を片づけた後、新宿京王の屋上でビール。青空に突き刺さる高層ビルに囲まれながら、そんな景色を眺めながらビールを飲むのは、とても気持ちよい。が、日が射さなくなるととたんに寒くなる。その後、東京「美少年」（←日本酒が結構揃ってる店）で飲む。こりゃ、体調悪化するわけだ。

■愛がなくちゃね　

　「高岡凡太郎の作品の典型のような、このぼんやりと暖かい連載漫画を、ある日読んでいて、ぼくは、ふいに感動してしまった。
　--- 赤ん坊だった娘がだんだん大きくなり、初めて幼稚園にいく日、一緒についていった、娘しか目に入らない高岡は、娘が先生から呼ばれて大きな声で返事をしたので、嬉しくなってしまう。
　彼は、こう書いている。
　　　　それでも少しだけ周りを観察すると…
　　　　教室の外でハンカチで目元をふいているお母さんを見つけました
　　　　きっとあのお母さんの子供も大きな声で返事をしたのだと思います
　そして、廊下で、ほかのお母さんたちと離れて、そっと涙をふいているお腹の大きい若い母親の絵が描いてあった。 ---
　ぼくは、突然、心動かされて、泣きそうになってしまった。
（中略）
そうだ。高岡凡太郎には、愛がある。ぼくがずっと彼を好きだったのは、きっとそれが理由だったのだ。」
from いしかわじゅん　漫画の時間

■IEのフォントサイズを一時的に変更する「ちょこっと 文字サイズ」　

　これはとっても便利そう。

■Tech総研「未来の可視化」編　

　「思いこみパワーで未来が見える」ニュースの中から、今日は「未来の可視化」に関するニュースがTech総研で公開です。いえ、実際には「過去と未来と現在の可視化」の三つのニュースです。過去を眺め、未来を眺め、そしてその境界にいる今現在を可視化して眺めてみるニュースです。色んな道具を使って可視化された過去・現在・未来を眺めて、何かを、例えば良し悪しでも考えてみることにしましょうか。あるいは、考え無しにただ眺めてみるのも良いかもしれませんね。

　ちなみに、男性の場合には、マイクロスコープで自分の毛根を可視化したりしてはイケマセン。哀しい現実が見えて、さらに暗い未来が想像されてしまうので、気分が滅入ること間違いなしです。

■道端の花　

■n年前の今日から「愛がなくちゃね」　

　ほんの三年前の今日から。「愛がなくちゃね」

ぼくは、突然、心動かされて、泣きそうになってしまった。そうだ。高岡凡太郎には、愛がある。ぼくがずっと彼を好きだったのは、きっとそれが理由だったのだ。

■現在の世界　

　「考え無しにただ眺めてみる」と書いた後、夜のニュースで「中東で起きている現在」の映像を見る。考えることを止めたくなる現在の景色。

■Graphic Organizer Makers　

　様々な図やチャートをオンラインで作成することができるGraphic Organizer Makers.コンセプト図や、ベン図や、時系列チャート…を一瞬で作成する。とにかく便利。

■PearPC - PowerPC Architecture Emulator　

　MacOS Xも起動する、PowerPCプラットフォーム・エミュレータのPearPC - PowerPC Architecture Emulator. from スラッシュドットジャパン

■裾野　

　富士と箱根の麓の裾野市で。

■QuartzComps　

　QuartzComps.

■「実は裏付けの無い最高速度」　

　「実は裏付けの無い最高速度」

■経済学って何ですか？「金で買えないものはない？(仮題)」　

　東京大学院総合文化研究科の松原隆一郎 教授（社会経済学・相関社会科学専攻）に先日話を伺いに行った。ホワイトボードにたくさんメモを取りながら話を聞いた。今日、その原稿を編集者宛に送付(リリース)した。ホワイトボード4面分のラクガキと、テープから起こした1万5千字ほどの文章をまとめ直して4千字だ。…たくさん内容を削ったが、興味深い内容も多かったので、私のメモ書き分はいずれ出していくことにしたい。特に、原稿にできない「曖昧な内容」こそが興味深かったりすることも多いわけだし。

　そういえば、これから何人かの経済学関連の人に話を聞きに行こうと考えた時に、自分の中で決めたことが一つある。それは、「一つの定義・考え方があるという期待・思いこみ・態度」は話を聞き原稿を書く中では一切捨てよう、ということだ。これから色んな話を聞いていく中で、その人ごとに違う意見・違う見方・違う言葉の定義をするだろう。私は単純理系？おバカのせいか、どうしても「シンプルな一つの定義・考え方がある」というように行動してしまいがちだ。しかし、この原稿を書く中では、そういう態度はゴミ箱の中に放り込んでおこう、と決めている。だから、もしかしたら、毎回食い違うことを書くことになるのかもしれない。いや、きっとそうなるに違いない。

■裾野・下丸子・秋葉原　

　自分の参考にしようと、ノートPC選び＆電子工作勉強のため秋葉原に行く、という人について夜秋葉原へ。夜ThinkpadにUSBを繋いだ途端に電源がブシュッと切れた。結局、電源が入るようにはなったけれど、USB周りはお亡くなりになっていた。まさか本当にノートPC選びが自分の参考になるとは…。

■続・腹部全脂肪面積減少のヒミツ　

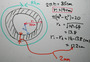
　「腹部全脂肪面積減少のヒミツ」を書いた後に、もしかしたら「腹部全脂肪面積」というのは、腹部の断面を撮影した際の「脂肪の断面積」を表しているのかもしれない、とふと考えた。つまり、右の胴体輪切り画像で言うところの「斜線部分＝腹部全脂肪面積」なのかもしれない、と考えた。

　腹部断面の脂肪断面積を「全脂肪」と言うのも不思議な感じがするし、それを「面積」と言うのもまた奇妙な気がするけれど、ふとそう考えた。そこで、「腹部全脂肪面積」が腹部断面における「脂肪の断面積」だった場合に、

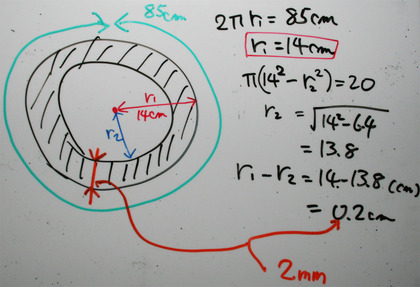
20cm^2ほどの「腹部全脂肪面積」減少

　すると、たとえばウェスト(腹部周囲長)が85cmの人であれば、20cm^2ほどの「腹部断面積」の変化は、腹部の半径（脂肪厚み）が2mm減少することに相当することがわかる。ということは、「腹部全脂肪面積」＝「腹巻で腹部を巻くようにしたときの円筒状の部分の表面積」とした時の昨日の計算結果、すなわち、腹部の半径（脂肪厚み）が1.6mm減少する、という結果と大して違いがないものになる。

　……とはいえ、脂肪厚みが2mm弱減少する、つまり、ベルトの穴で一つ細くなる、というのは（それが本当であれば）結構魅力的である。一体、香るブラック ブレンディの「コーヒー豆マンノオリゴ糖」のちからが示す「腹部全脂肪面積」は何を示しているのだろうか。

■8インチ空気タイヤ版A-bike(風自転車)用の100円輪行バッグ　

　8インチ空気タイヤ版A-bike(風自転車)を、付属の鞄に入れて持ち歩いています。付属の鞄は、すぐに穴が空いてしまったりしたので、穴を黒いガムテープでふさぎながら、持ち歩いています。A-bike（やA-bike風自転車）は、バッグに入れさえすれば、その中に自転車がまさか入っているとは思えないサイズになりますから、本屋でも電気店でも自転車を持って気楽に入ることができます。

　とはいえ、自転車を組み立てたり・畳んだりする時間があまりに短いので、バッグに入れる時間が長く感じられるようになってしまうのです。お店に入るというわけでなく、ただ電車に乗って自転車を持ち歩く程度なら、もっと簡単で小さく軽い輪行セットが欲しくなります。・・・そこで、いつものように、100円ショップへ行って、安くて簡単に自転車を持ち歩くことができる道具を選んでみることにしました。

　今回のテーマは、「（比較的丈夫で長持ちする）簡単風呂敷」です。100円ショップで見つけた100cm×70cmの前掛けを買い、風呂敷状に使いA-bike(風自転車)を包むような「輪行袋」を作ってみました。つまり、「腹巻や腹帯を使ってA-bike(型自転車)を輪行する」で書いたような、「自転車を苦労して袋に入れる」のではなく「自転車をシートで気楽に包んでみよう」というアプローチです。

　それが、下の写真の「輪行袋」です。「100円」というコストを考えた上での、コストパフォーマンスを考えれば、なかなか良い感じです。

■オブジェクト指向のRubyに、数式処理ソフトウェアMathematicaの機能を自然な形で取り入れてみよう!?　

　「Rubyで数独ソルバを書いてみる」でMathematicaで書かれたコードをRubyに翻訳してみました。その作業をしながら考えたことは、「Mathematicaの機能をRubyに自然に取り込むとしたら、一体どういう言語仕様になるのだろうか」ということです。すべてのものが「リスト」であり、基本的に関数型言語であるMathematicaの機能を、多くのものを「オブジェクト」として扱うオブジェクト指向のRubyに（Rubyになじんだやり方で）取り入れるとしたら、一体どんな記述になるのだろう？という疑問です。

　RubyとMathematicaを繋いだものとして、Ruby/Mathematicaがあります。Ruby/Mathematicaで「Cos(x)をxで積分した結果」を求めるコードは下のようになります。

math=Mathematica::Mathematica.new.start
puts math.eval_foreground('Integrate[Cos[x], x]')

　そこで、頭の整理がてら、もしもMathematicaのコードをRubyに溶け込ませるとしたらどうなるかを考えながら、「Mathematicaの機能を(.NETベースの)IronRubyに取り込むコード」をつらつら書いてみました。

　書いたコード（ライブラリ）は後述することとして、まずは、そのコードを使った例を紹介してみることにします。たとえば、「Cos(x)をxで積分した結果」を求めるなら、こんな感じの記述になります。

p 'x'.Cos.Integrate 'x'

　あるいは、'2 x + 3 == 0'という方程式を、xについて解くなら、

'2 x + 3 == 0'.Solve 'x'

　同様に、「（Rubyネイティブの!）配列"[[1,2,3],2,3]"について、それぞれのサイン関数を求め、数値化する（その結果を出力する）コード」なら、こんな具合です。

p ([[1,2,3],2,3]).map.Sin.N

p 3.Times(10).Plus 5

　さて、オブジェクト指向のRubyにMathematicaの機能を自然な形で取り入れるために、試しに書いてみたコードは、下のようになります。

　…下のコードを要約すると、メソッド名が見つからない場合に呼ばれるmethod_missingで、「見つからないメソッドがあった場合には、その命令をMathematicaに投げちゃえ」というだけのコードです。つまりは、単に(Ruby上で)未知のメソッドを「右(Ruby)から左(Mathematica)に受け流す」という「ムーディ勝山」方式…ということになります。しかも、オブジェクトの総本山、Objectクラスにその「ムーディ勝山」メソッドをいきなりMix-inしてしまう…という、とんでもないコードです。一発ネタ的コードとして、楽しんで頂けたら幸いです。

# 2010/05/12 jun hirabayashi jun@hirax.net

class Mathematica
  require 'Wolfram.NETLink'
  include Wolfram::NETLink
  # ここにMathKernel.exeへのパスを記述する
  PAR="-linkmode launch -linkname 'C:...\\MathKernel.exe'"

  def Mathematica.to_m(array)
    strArray=[]
    array.each do |item|
      if item.kind_of? Array
	strArray＜＜Mathematica.to_m(item) 
      else
	if item.kind_of? String
	  strArray＜＜'"'+item+'"'
	else
	  strArray＜＜item
	end
      end
    end
    '{'+strArray.join(',')+'}'
  end
  
  def Mathematica.to_a str
    require "JSONParser" 
    jsonParser=JSONParser.new
    s=str.gsub(/, ([^{]{1})/,',"\1')
    s=s.gsub(/([^}]{1}),/,'\1",')
    s.gsub!(/\{([^{]{1})/,'["\1')
    s.gsub!(/([^}]{1})\}/,'\1"]')
    jsonParser.parse s    
  end

  def Mathematica.callback
    proc {
      @kernelLink.EvaluateToInputForm 'MVClose[]',0
    }
  end

  def initialize()    
    ObjectSpace.define_finalizer self,Mathematica.callback
    @kernelLink=MathLinkFactory.CreateKernelLink PAR
    @kernelLink.WaitAndDiscardAnswer
  end
  
  def do(q)
     @kernelLink.EvaluateToInputForm q,0
  end
  
end

module MathematicaModule
  def method_missing(name, *args)
    $mathematica=Mathematica.new unless $mathematica
    if self.kind_of? Array
      obj=Mathematica.to_m(self) 
    else
      obj=self 
    end 
    if name.to_s
      results=$mathematica.do( [name,'[',
          ([obj]+args).join(','),']'].join('') )  
    end
    return results
  end

  def To_a
    Mathematica.to_a self
  end
end

class Object
  include MathematicaModule
end

■「シャボン玉」送信を継続中　

　初夏の空にはシャボン玉が似合います。 だから、「シャボン玉」始めました。 今日も、ポルトガル語で石けんを指す「シャボン」を溶かした液に風を吹き付け、小さな閉曲面を空へとたくさん流しています。

　はじけたシャボン液たちが、向けたレンズに張り付いて、シャボン玉が反射する光を幻想的な姿に見せています。空に浮かんだシャボン玉の姿が、遠くの街にも届くことを願いつつ、「シャボン玉」送信を継続中です。

■制服スカートがめくり上がる力は「ほぼ１００〜１５０グラム重」で、風速でたとえると秒速１０ｍ弱…という法則を裏付ける実験経験　

　スカートがめくり上がるのに必要な力の大きさをを計ったことがある人は多くはないかもしれません。けれど、実際に計ってみると、およそ１００〜２００グラム重の力がかかると、スカートがめくれ上がってしまうという実験をしたことがあります（チェック柄の制服スカートをめくり上げる力は「ほぼ１００〜１５０グラム重」という豆知識）。

　また、送風機を動かしつつ、スカート周りにかかる力を測定する状況は少ない…と思われる人もいるかもしれませんが…実際には、そういう送風機とスカートがカップリングされた状況は結構多いものです（個人の印象・意見です）。実際に、そうした実験をしてみると、「風でめくれるスカート」の科学！「涼しく晴れた朝の地下鉄駅をドジっ娘が走る」とスカートは必ずめくれる!?の法則に書いたように、秒速６〜１０ｍくらいで、スカートがめくれ上がり始めるという…当たり前の結果になります。

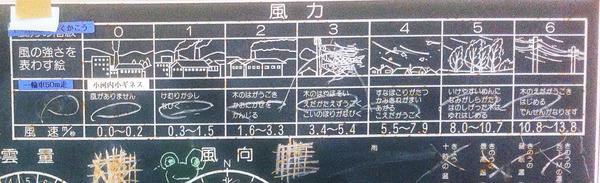
　山奥の小学校でスカートと送風機を抱えていると、小学校の黒板に、風力と風の強さが図示されていました。制服スカートがめくり上がる「ほぼ１００〜１５０グラム重」の力は、「砂ぼこりがたち、紙切れが舞い上がり、小枝が動く」程度と書いてあります。…さてさて、あなたの経験上は、その対応関係には違和感ありませんでしょうか？