2000-08-13[n年前へ]
■WEBの時間、サイトの寿命 
ゆっくり長く続けましょうか?
以前、
でロゲルギストが- 第五物理の散歩道 ロゲルギスト著 岩波新書 「通信を考える」
- その系の情報処理の単位時間
- その系の信号の伝わる速度
- その系の空間スケール
- 空間スケール < 情報処理の単位時間 × 信号の伝わる速度
- 大人数から構成される企業のスピードは、少人数から構成される企業のそれには遙かに及ばない
ところで、ロゲルギスト達はある系の「単位時間・信号伝達速度・大きさ」の間の関係について、
- 「単位時間・信号伝達速度」を入力値として、「大きさ」を考える
- 「大きさ・信号伝達速度」を入力値として、「単位時間」を考える
さて、寺田寅彦が「単位時間・信号伝達速度・大きさ」について、さらにどのようなことを展開していたかというと、それはある系の「大きさ・寿命」についての関係である。寺田寅彦は
- 空想日録 三 身長と寿命 (寺田寅彦随筆集 第四巻 岩波文庫 小宮豊隆編)
- 人体感覚について振動感覚の限界を調べた実験データ、 - 人は自らの体の固有振動周波数の振動に対してもっとも過敏である- 、というものをきっかけとして、
- 生物の時間の長さの単位は相対的なものである
- ある系の「時間の長さの感覚 = 相対的な単位」はその系の固有周期と密接な関係がある(振り子時計なんてわかりやすいだろう)
- ある系の「寿命」を測る単位は、その系の「時間の相対的な単位」、すなわち、その系の固有周期だと想像してみよう。
- その場合、ある系の固有周期はその系の大きさに比例するから、大きい動物ほどその系の「時間の相対的な単位」は長いものとなり、見かけ上の「寿命」はその動物の「大きさ」に比例するだろう。
なるほど、サイズが小さい動物(すなわち固有振動の波長の短い動物)にとっては、ほんの小さな変化も大きな変化である。ということは、その動物の感じる「時間単位」は短くなければ、生き残れないだろう。逆に、サイズの大きな動物は俊敏な動きはできないわけで、その動物の「時間単位」は長くならざるをえないだろう。
ゾウのような大きい動物は「時間単位」が長く、一見「寿命」が長いように見え、ノミのような小さな動物は「時間単位」が短く、一見「寿命」が短く見えるというわけだ。実は、ゾウもノミもその動物自身の「時間単位」を基準にすると、同じ寿命を生き抜いているということになる。
本川達雄の中公新書「ゾウの時間 ネズミの時間」では- 体重の4分の1乗に比例して「その動物の時間単位=生理的時間」が長くなる-と述べられているが、昭和八年に既に寺田寅彦は体重は身長の3乗に比例する、逆に言えば体重は身長の3分の1乗に比例するから、「体重の3分の1乗に比例して時間が長くなるだろう」と想像を巡らせているのである。素晴らしい、想像力である。
さて、寺田寅彦はロゲルギストと違って、「単位時間・大きさ」については言及しているが「信号伝達速度」については触れていない(その替わり、さらに「寿命」にまで触れているわけであるが)。もっとも、私があえて書き加えてみるならば、ある系の固有振動にはその系の中での弾性が密接に関係するし、弾性はその中での弾性波の速度も密接に関係する。つまり、ある系の固有振動の周期というものには「その系中での波の伝達速度」が暗に隠されていて、寺田寅彦は単にそれを一定とおいていたわけで、寺田寅彦が述べた内容は実はロゲルギスト達の述べた内容を包括している、と私は思うのである。
このような「単位時間・大きさ・信号伝達速度・寿命」に関する話は動物に限るものではない。
- ロゲルギストが「信号伝達速度=光速度」として、「処理速度を確保する」ための人類の行動範囲について論じたり、
- 私(いきなり自分を例に出すのも何だが)が「信号伝達速度の変化」と「大きさ(人口)の変化」から人類の処理速度の変化について論じたり
さて、前振りが長くなった。前回、
では、単に「信号伝達速度の変化」と「大きさ(人口)の変化」を並べて「処理速度」の変化について考えてみただけだった。今回は寺田寅彦が考えたのと同じく、「信号伝達速度」と「大きさ(人口)」から「寿命」が決まると考えることにより、「人類」の「寿命」の変化について考えてみることにしたいと思う まずは、前回使った「人類の大きさ=人口」の変化が次のグラフである。ただし、この人口は全然正確ではないし、むしろかなり不正確なものであることは先に断っておく。ここでは、細かな値を使うのが目的ではないので別に構わないだろう。
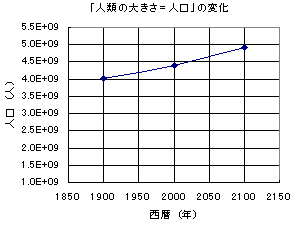 |
そして、「人類」の中での「情報伝達速度」の変化を示したものが次のグラフである。この速度が「人類」という集合体の中での波の進行速度を決めるのである。
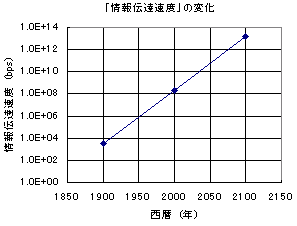 |
それでは、「人類」という集合体の固有振動はどうやって扱うかというと、この
- 「人類の大きさ=人口」
- 「情報伝達速度」
- 人口 / 情報伝達の速度
その、人口 / 情報伝達の速度 = 「人類の固有時間」を計算してみたものを次に示してみよう。
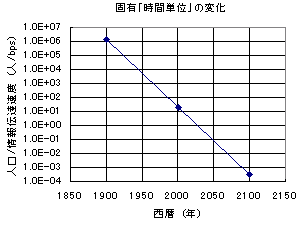 |
こうしてみると、人類というヒトの集合体においては、どんどん時間の流れは速くなり、それに応じて見かけの「寿命」は短くなっている、ということがわかる。人類はまさに生き急いでいるのである。もし、この流れを止めようと思ったら、どうしたら良いだろうか?それには、今回の計算から言えば情報転送速度を遅くするか、人類の大きさを大きくするしかない。情報転送速度を遅くするのはなんとも後ろ向き(byわきめも)だし、人口を減らすというのもなんとも後ろ向きだ。だとしたら、宇宙へでも人類が進出して、人類の空間的なスケールを大きくしていくしかないのだろうか?これもまた難しい話である。
さて、最近、大好きなWEBサイトが閉鎖してしまったり、更新速度が遅くなっていたりしていて少しさみしい。だけど、もしかしたら各WEBサイトにも、「更新速度が速いと、WEBサイトの寿命が短い」なんて法則が実はあるのかもしれない。更新速度が速いということは、そのWEBサイトの固有時間が速く流れているということで、限られた寿命をどんどん使い果たしているのかもしれない。
だとしたら、更新速度が遅いということはそのWEBサイトの寿命が長くなるということだから、それはそれで良いのかなぁ、などと思ってみたりする。「太くて短い寿命」も「細くて長い寿命」も実は本人からすればどちらも同じ長さなのかもしれないけれど、外から見ている私は「細くても良いから長く続いて欲しいなぁ」なんて思ってもみたりするのである。
2000-11-26[n年前へ]
■ブランコの中の∞(無限大) 
なんで一体漕げるのだろう?
公園のブランコというのは、何故かとても不思議な雰囲気を持っている。ホントにうるさいくてたまらないくらいのガキんちょ達が、アクロバットのようなスゴイ技を見せていたりする。それは、まるで上海雑伎団を見ているような気分になる。小さな子がなかなかブランコが漕げず、ブランコの上で宇宙遊泳のように四苦八苦しているのを見ているのも思わず笑ってしまうくらいに可愛らしいものだ。もちろん、そこは子供の領分というだけではなくて、黒沢明の「生きる」の主人公がしていたように「大人がブランコに座って揺れていたり」すると、思わずその人の陰に隠れている物語を想像したりしてしまう。ブランコの周りというのはそんな不思議な雰囲気を持っているのだ。
やたらにブランコを漕ぐのが上手いガキんちょもいる一方で、全然ブランコを漕げず四苦八苦する子供もいる。ブランコを漕ぐコツを覚えるのもなかなか大変そうである。考えてみれば、ブランコは一体どういう風に漕ぐものなのだろう?口で上手く説明できる人がいるだろうか?
それに、そもそも私たちはブランコを何故漕ぐことができているのだろう?
いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか?という手紙で始まるのは加納朋子の「ななつのこ」だが、「何故、リンゴは落ちるのかという謎」と同じく、「ブランコの漕ぎ方の謎」だってとても不思議だ。いつも目にする公園のブランコを、私たちは一体どうやって漕ぐことができているのだろう?
いつだって、どこでだって、謎はすぐ近くにあったのです。
何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。
もちろん、「何でブランコの漕ぎ方が不思議なのさ?」と言う人も多いだろう。その中には理路整然とブランコの漕ぎ方を説明してくれる人もいるだろう。そして、「特にブランコの漕ぎ方をじっくり考えたことなんかないもんね」という人も多いに違いない(私だけかもしれないが)。そこで、まずは「ブランコの不思議」を簡単に書いてみることにしよう。
次の図は「ブランコを漕いでる子供」である。
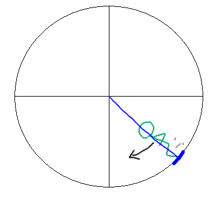 |
この子供が何もせず立っているだけ(あるいは座っているだけ)だったら、どうなるだろうか?それはもちろん、単なる振り子と同じくようにブランコは動く。もしも色々な摩擦がなければ、まったく同じように動き続けるだけだし、摩擦力があればブランコの動きはただ減衰していくだけである。つまり、子供が何もしなければ、ブランコの動きは「遅く・小さく」なることはあっても、ブランコが「速く・大きく」なることはないのである。
だからブランコを速くするためには、「ブランコに乗ってる子供がブランコを漕がなければならない」わけであるが、ブランコに乗ってる子供は一体どんなことができるだろうか?
次に示す図は「ブランコに乗ってる子供を中心にとった座標軸」を描いてみたものだ。この図の中で直交する二つの軸を描いてある。つまり、
- ブランコの動きの中心を向いている軸A
- 軸Aに直交する、つまりブランコの進行方向(あるいはその逆方向)を向いている軸B
 |
ところが、実は「ブランコに乗ってる子供」はこの二つの軸の内の片方、軸Aに対しての動きしかできない。何故なら、軸B方向に対しては「ブランコに乗ってる子供」動きの支えになるモノが全然無い。だから、ツルツル滑る氷の上では全然動けないのと同じく、「ブランコに乗ってる子供」はその方向には動けないのである。もし子供がその方向に動こうとして体を動かしたりしても、結局子供の重心はその方向には全然動かないのだ。
それに対して、ブランコの動きの中心を向いている軸A方向に対してはブランコの鎖も座っている(あるいは立っている)板が支えになるわけで、その方向に対しては「ブランコに乗ってる子供」は動くことができる。
というわけで、ブランコの上では「ブランコの動きの中心を向いている軸A」方向にしか動けないわけであるが、その方向というのはブランコの進行方向に対しては直交している。つまり、ブランコを漕ぐためには、「ブランコの進行方向に対して直交している方向に動く」しかないことになる。
ここまで書くと、ブランコの不思議が判るハズだ。ブランコを漕ぐ、つまりブランコを軸B方向の速度を上げたいのに、我々は「軸Bに対して直交している方向に動く」ことしかできないのである。一体何故、軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増すのだろうか? この謎「ブランコの不思議」を、ゆっくり考えてみることにしよう。
まずは、ブランコに乗ってる子供が立ち上がったりして、「ブランコの動きの中心を向いている軸A」方向に動いた場合、何が起きるだろうか?
 |
「ブランコの動きの中心を向いている軸A」方向に動くと、ブランコの鎖の長さが短くなることと同じである。すると、回転しているブランコの鎖が短くなるわけで、そうするとブランコの速度は速くなる。何故なら、角運動量が保存されるからである。ちょうど、スケートのフィギア競技の選手が回転中に伸ばしていた手を縮めると回転数が早くなるのと同じだ。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの半分だけ(とんでもない身長の子供だ!)上がれば、ブランコの速度はもとの速度の倍になるのである!
ということは、少なくともこの瞬間は「軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増す」わけであるが、これでブランコの漕ぎ方を納得するにはまだまだ早いのである。確かに、「ブランコの動きの中心を向いている軸A方向に動く」とブランコの速度は増すわけであるが、それはその瞬間だけである。ブランコの上で「立ち上がり続ける」なんてことはできないわけで、速度が増し続けるわけではないのである。
もしも、「もう一度ブランコの上で立ち上がるために、すぐに低い姿勢に一旦戻ったり」したら大変だ。ブランコの鎖の長さが長くなるのだから、今度はブランコの速度は遅くなってしまうのである。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの二倍だけ(つまりさっき立ち上がった逆の動きである)下がれば、ブランコの速度はもとの速度の1/2になってしまうのだ!
これでは、結局さっきの速度が二倍になったことは帳消しになってしまう。つまり、「単純に」角運動量の保存を考えるだけではブランコの速度を(長い間にわたって)早くしていくことはできないわけだ。
このままでは、「ブランコを漕ぐことなんか不可能である」という結論が出てしまいそうになるが、ブランコを漕いでる子供達はイッパイいるわけで、そんな結論を受け入れるわけにはいかない。彼らがみんな超能力でブランコを漕いでいるわけもないのである。まだまだ見落としていることがあるので、ブランコの不思議の謎が解けないだけのハズなのだ。
そこで、ちょっと考えてみると「とんでもなく単純なこと」を見落としていたことに気付いた。それは、「タイミング」である。例えば、ブランコの速度がずっと同じであるすると、
- 初期のブランコの速度 = 10
- 重心位置を高くして 10 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- 重心位置を低くして 10 X 1/2 = 10 (何てこったい、速度が半分になっちまったか!)
- 初期のブランコの速度 = 10
- 重心位置を高くして 0 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- そのあとブランコの速度 = 0
- 重心位置を低くして 0 X 1/2 = 0 (0が0になっても全然変わってないもんね!ヘヘン!)
人生何事もタイミングが重要である。失恋した男性や女性にタイミングをわきまえた「恋のハイエナ」達が寄ってくるのと同じく、またお金に困っていると何故かサラ金の広告が目の前にチラチラするのと同じく、ブランコを漕ぐにはやはりタイミングが重要なのだ。
なるほど、考えがまとまってきた。このイキオイでそのまま「ブランコの理想の漕ぎ方」まで考えてしまおう。
まず、「重心位置を高くしてブランコの速度早くする」にはできるだけ速度が速い瞬間に行うのが良いだろう。倍率が確定している賭なのだから、元金はあればあるほどおトクである。1万円×2=二万円では1万円しかもうからないが、一千万円×2=二千万円では一千万ももうかるのだ。ブランコの速度が速い瞬間に立ち上がれば、一番おトクに速度を増すことができるのである。
もちろん、ブランコの速度が速い瞬間といえば、明らかにブランコが一番下にきた瞬間である。つまり、ブランコが一番下にきた瞬間に立ち上がれば「一番おトクに速度を増すことができる」わけだ。しかも、その瞬間は鉛直に重心を持ち上げることになる。つまり、位置エネルギーを効果的に増加させることができるわけだ。結局、この時に増加させた位置エネルギーは後で、運動エネルギーに変換されるわけで、結局これがブランコの運動の源となるのである。
そして、「次にもう一度立ち上がるために一旦低い姿勢に戻る瞬間」=「速度が遅くなる瞬間」はブランコが停止しているときであれば何の問題もない。ブランコはもともと止まっているんだから、その速度が何分の一になったって全然気にしないもんね!となるわけだ。そのタイミング= ブランコが止まる瞬間といえば、もちろんブランコが最高地点まで上がった瞬間である。つまり、ブランコが一番上にいった瞬間に低い姿勢に戻れば全く減速無しに次の加速に備えることができるわけである。しかも、その時には実は運動エネルギーを位置エネルギーに変えることで、隠し財産にしているわけで、もう汚い政治家のマネーロンダリングのような見事な方法なわけだ。
というわけで、
- ブランコが下に来たときに(立ってる場合は)足を伸ばして立ち上がったり、(座ってる場合は)足を曲げたりすることにより高い位置に重心を持ってきて(しかも、重力に逆らって重心を上げるため位置エネルギーが増加する)
- ブランコが上に行ったときにその姿勢を元に戻す
それでは、確認のためにそのやり方で本当にブランコが漕げるのかどうか、シミュレーション計算を行ってみた。ブランコの動きは振り子運動だが、振れ幅がとても大きいので、cosx≒xというような近似をする単振動としての扱いはできない。そこで、楕円積分の計算を行わなければならない。が、私が自分の力でできるかどうかはともかく、そこはMathematicaに解かせればイッパツである。もう、驚くくらい簡単なのである。自分の力で解いていないところが、実に悲しい現実ではあるが、それが現実なのだからしょうがない。
というわけで、ブランコの動きのシミュレーションをしてみた結果が次のグラフである。「ブランコに乗ってる子供」の漕ぎ方としては、以下の三つ
- 何もしない場合
- ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合
- ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合
 → ブランコの動きはず〜と変わらない |
ブランコが上にきたあたりで座り込んだ場合  → ブランコの動きはどんどん大きくなる 「やったぜ、これが理想の漕ぎ方だぁ。」 |
ブランコが上にきたあたりで立ち上がった場合  → ブランコの動きはどんどん小さくなる 「なんてこったい、遅くなっちまったぁ。」 |
この結果から、ちゃんと1.の「何もしない場合」は「ブランコの動きはず〜と変わらない」し、理想の漕ぎ方であるハズの2.の「ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合」は「ブランコの動きはどんどん大きくなる」し、最悪の漕ぎ方であるハズの3.の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合」には「ブランコの動きは逆にどんどん小さくなってしまう」ことがわかる。というわけで、今回考えた「ブランコの不思議= 漕ぎ方」はシミュレーション計算結果からも確かめることができたわけだ。
ところで、こういったタイミングを考えながらパラメーターを変えることで動きを大きくしたりすることは「パラメータ励振」と呼ばれる。ブランコの漕ぎ方はその「パラメータ励振」の応用のひとつである。「何故、リンゴは落ちるのかという謎」には重力という基本的な物理現象が隠されていたが、それと同じく、「ブランコの漕ぎ方の謎」にも「パラメータ励振」という物理現象が隠されているのだ。次回以降も、この「パラメータ励振」を手がかりにいくつかの「身近な謎」に迫ってみたい、と思うのである。
さて、公園でブランコを漕ぎまくる子供をもし見かけたならば、ぜひ横から子供の動きを見てやってもらいたい。きっと、その揺れ動くブランコの中にはこんな∞(無限大)の形が見えるハズだ。天まで上ろうとする「ブランコの秘密」はその「ブランコの中の∞(無限大)」に隠されていたのである。子供も含めて人間の可能性は∞(無限大)だと私は思うが、ブランコの揺れる動きから、そんなことを考えてみるのも少し面白いのではないだろうか? それとも、ちょっと考え過ぎかな。
2003-11-04[n年前へ]
■手書きで数学・物理を遊んでみる 
Microsoft Researchの「数式を書くとそれが認識され、例えば数式を書いて振り子をターゲットとして指定してやると振り子が揺れるようすをアニメーション表示してくれるようなソフト」Math Padとか、「手書きの画像で物理シミュレーションができるソフトウェア」のMagic Paperとか面白そうなソフトの記事。
例えて言うと、カルキングをもっと気楽にした感じかな。
2008-06-26[n年前へ]
■各席独立「振り子制御」の自動車はいつか登場するか? 
 BOSEのボーズ・アクティブサスペンションの公開写真・動画などを見ると、車体を水平に保つように制御していることがわかる。だから、荒れた路面の上でも乗客は揺れを感じないことになる。しかし、コーナリング時を考えると、車に乗っている人は左右へ揺れ動かされるような遠心力を感じてしまう。
BOSEのボーズ・アクティブサスペンションの公開写真・動画などを見ると、車体を水平に保つように制御していることがわかる。だから、荒れた路面の上でも乗客は揺れを感じないことになる。しかし、コーナリング時を考えると、車に乗っている人は左右へ揺れ動かされるような遠心力を感じてしまう。
もちろん、ボーズ・アクティブサスペンションのような、車体を水平に保つような制御をかけることがない場合には、つまり、カーブ外側に傾く(ロール)ような場合には、左右へ揺れ動かされるどころでなく、それと同時に、車の乗員は上下に変化する加速度を受け、上に投げ出されるような力を感じてしまう。カーブ時にカーブ外側上方に体が浮かび上がる感覚というのは、かなり気持ちが悪く・不安になるものでもある。逆にいえば、そんな感覚を受けた運転手はスピードを(車の動きへの不安から)当然落とすことになる。だから、乗り心地はそれに比べればずいぶん良いに違いない。
 カーブを高速に走らなければならない特急などでは、列車車体を水平に保つのではなく、カーブ内側に傾けるような「振り子制御」を行うものもある。カーブ内側に列車の車体を傾ければ、カーブ時に外に引っ張られる遠心力が乗客の足もとの方向へと働くことになる。ということは、振り子制御をすれば、左右に揺れ動かされる感覚が減ることになる。さらには、カーブ時に受ける感覚が、「カーブ外側上方に体が浮かび上がる」ようなものではなくて、「体が下方向に(抑え)固定される」ような感覚に変わる。つまり、乗客がより「安心」を感じるような動きにさえ変わる、ということである。
カーブを高速に走らなければならない特急などでは、列車車体を水平に保つのではなく、カーブ内側に傾けるような「振り子制御」を行うものもある。カーブ内側に列車の車体を傾ければ、カーブ時に外に引っ張られる遠心力が乗客の足もとの方向へと働くことになる。ということは、振り子制御をすれば、左右に揺れ動かされる感覚が減ることになる。さらには、カーブ時に受ける感覚が、「カーブ外側上方に体が浮かび上がる」ようなものではなくて、「体が下方向に(抑え)固定される」ような感覚に変わる。つまり、乗客がより「安心」を感じるような動きにさえ変わる、ということである。
それならば、車のサスペンションもそんな振り子制御をすれば良いか、というとそういうわけでもない。カーブ(コーナリング)時に「体が下方向に(抑え)固定される」ような感覚に変わってしまう、つまり、これまでとは逆に「安心」を感じるようになってしまう。これはあまり安全ではない。
まるで、タイヤのグリップ性能が増したかのように、あるいは、路面に適切なハングがついているかのように運転者感じてしまったならば、コーナリング時に適切な減速を行うことをしなくなってしまう可能性が高い。運行速度が厳密に守られている列車と違い、車の速度制御に対する運転者の自由度が高い車では、車の運転者の感覚に対し「車の状態」のフィードバックを適切に与える必要があるわけだ。車の状態に応じて、適切に「不安」「安心」を運転者に感じさせるのが安全なサスペンション設計である、ということなのだろう。
しかし、運転者以外の乗客にもそういった『車の状態に応じた適切な「不安」「安心」』を感じさせた方が良いかどうかは、判断が分かれるところだと思う。運転手と同じように車の揺れを感じた方が良いかもしれないし、それとは逆に、車の素直な状態を感じる・知ることもなくただ安心して乗車していることができた方が良いのかもしれない。
もし後者の考え、つまり運転者とそれ以外の乗客が受ける感覚も違った方が良いということになるならば、運転手とそれ以外の乗客に対する姿勢・上下位置制御が違った方が良いということになりそうだ。つまり、車の(少なくとも)運転席が車体と独立に「振り子制御」されるような自動車を作れば良い、ということである。
 そんな運転席と乗客席が独立に動く「振り子制御」自動車はいつか登場するだろうか?それとも、「運転手(席)」というもの自体が未来の車には存在せず、運転はすべて自動で行われるようになっていて、そんな各席独立「振り子制御」などそもそも必要なくなっているのだろうか。
そんな運転席と乗客席が独立に動く「振り子制御」自動車はいつか登場するだろうか?それとも、「運転手(席)」というもの自体が未来の車には存在せず、運転はすべて自動で行われるようになっていて、そんな各席独立「振り子制御」などそもそも必要なくなっているのだろうか。
2008-10-28[n年前へ]
■続 「電車の吊り手」のヒミツ 
「電車の吊り手」のヒミツ の続きです。
「電車の吊り手」の構造が以前とは、、90度違う方向にぶらさがるように変わっていることに気づきました。そんな吊り手を見ながら、その効果をラクガキをしつつ考えてみたのが、下図になります。
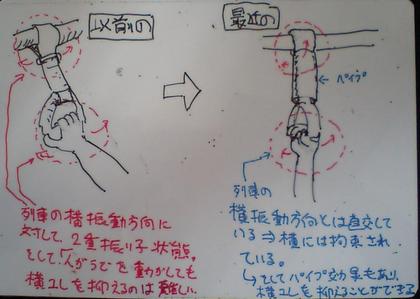
イラストにして見ると、以前の吊り手が「列車の横揺れ方向に対して、2重振り子状態」になっていることがわかります。また、吊り手の支持部と、吊り手の持ち手部が、いずれも列車進行方向に向いているために、横揺れをなかなか抑えることができないように(自分の経験から)思われます。乗客が腕を動かして揺れを抑えようとしても、吊り手に2カ所関節があるので、揺れを抑えるのは難しいように思えます。
しかし、最近の吊り手は(図のように)以前のものとは違うことがわかります。吊り手の持ち手部分が列車の横振動方向とは直行し、(さらに、吊り手のベルト部分がパイプに包まれていることもあり)列車の横揺れに対し、その揺れを抑えることが容易になったように思えます。
ここで、興味深いことは、吊り手のベルトをパイプで囲ったことの効果は別として、吊り手の持ち手部分の方向を90度変えたことで、「列車進行方向揺れ」には弱くなった・揺れやすくなったということです。つまり、列車が走るとき「ほとんどの時間は横揺れを感じる時間で、進行方向の揺れを感じるのは駅に発車・到着する時くらいなので、横揺れ抑制効果を重要視しよう」という判断をしたのでしょう。そういうメリット・デメリットを秤に乗せて行われる選択・技術改良・コスト変更にとても興味を惹かれます。
列車には、吊り手がたくさんぶら下がっています。そんな、吊り手と同じように、たくさんの吊り手が変化したように、そんな技術改良・コスト変更などは、きっとたくさんあると思います。そんなものを町中で見かけると、なぜか楽しく感じたりします。
