hirax.net::Keywords::「巡回セールスマン問題」のブログ

■サンタが街にやってくる

複数サンタクロースの巡回問題

　幼い頃、クリスマスの夜を清里の聖ルカ教会で過ごしたことがある。今では、「アイスクリーム」で有名になってしまった聖ルカ診療所の隣の教会だ。清里を通る小海線が蒸気機関車からディーゼル列車に切り替わった頃だった。私の住んでいた野辺山から一番近い病院がその聖ルカ診療所だった。今はどうなのか判らないけれど、あの病院の中の風景はまるで高原の療養所のようで（高原の診療所なのだから大して違いはないのだけれど）、とても不思議だった。

　さて、クリスマスの人気者と言えば、やはりサンタクロースである。世界中の子供達から待ち焦がれられ、プレゼントを配って歩くのだから、クリスマスイヴのサンタは大忙しなのである。一体、サンタクロースはどんな風にプレゼントを配って歩くのだろう、と思った私は「サンタクロースの巡回問題」について考察をしてみることにした。

　知らない人のために書いておくと、「巡回サンタクロース問題（TSP:TravelingSanta Problem)」というのは「巡回セールスマン問題(TSP:Traveling SalesmanProblem)」の特殊例である。そもそも「巡回セールスマン問題」というのは「n人の顧客の場所が与えられたとき、全ての顧客を一回ずつ経由して巡回する際に、移動距離が最小になる経路を求める。」という問題である。計算幾何分野で最もメジャーな話であって、カーマーカー特許などこれに関係するものである。つまりは、色々なものを配達する際には「配達経路を考えるのは実は結構大変なのだ」という問題なのである。
 

　これまで「巡回サンタクロース問題」を考えた人がいなかったか、と言うとそんなことはなくて、試しにinfoseekで"サンタ"AND"巡回"で検索すると、既に素晴らしい研究がなされている。それが

• サンタクロース研究
• ( http://www.geocities.co.jp/HeartLand-Suzuran/5872/santa.html )

である。サンタクロースの行動について詳細な考察がされており、その中で「巡回サンタクロース問題（TSP:TravelingSanta Problem)」について触れている。考察大好き人種ならとても楽しめる内容である。
 

　そこで、そんなこれまでの「巡回サンタクロース問題」に関する研究を踏まえながら、「できるかな?」ではさらに「サンタクロース巡回問題」を考え、そして、できることであればサンタの隠された真実にさらに迫ってみようと思う。「サンタクロース巡回問題」の中には、サンタクロースの真実に近づく鍵が含まれている、と私は何故か感じるのである。

　まず、始めに問題提起をしてみよう。

　「果たしてサンタは一人なのか？」

　どのような事件においても(別に事件ではないが)、単独犯か複数犯かというのはとても重要な問題である。犯人が単独犯か複数犯かで証拠の指し示す意味は異なってくる。サンタは一人、と私たちは何故か思い込んでいるが、そんな先入観は正しい捜査のたまには捨てる必要がある。

　そこで、まずはサンタの歴史から調べてみると、Ｓａｎｔａさんの起源、クリスマスページ!によれば、サンタクロースの起源であるSt.Nicolausは西暦4世紀頃の人であるという。その頃の人口は現在よりもはるかに少なかった。それは、サンタの労働量がはるかに少なかったということだ。なるほど、この時代であれば、サンタは一人でも不思議ではないかもしれない。

　とはいえ、Ｓａｎｔａさんの起源の中の色々なサンタの目撃情報を見ると、本当にサンタは一人なのか疑問を感じるのもまた確かである。色々なサンタが目撃されている、ということはサンタは実は複数犯の可能性が高いのではないだろうか？

　また、世界の人口は人口増加に示されている全世界の人口増加の様子を見れば明らかなように爆発的に増えている。ちなみに、そこに示されているグラフを対数軸にし、近似式を加えたものが以下である。
 

全世界の人口増加の近似グラフ

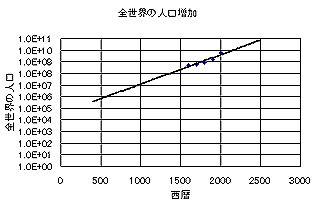　St.Nicolausのいた西暦4世紀頃に比べて現在の人口は4桁、すなわち、10000倍に増えている(近似式によれば。ホントのところは知らない)。これでは、サンタクロースは年々仕事量が驚異的に増えていることを意味する。もし、サンタが単独犯であるとするならば、過労死はまぬがれそうにない。

　サンタの単独犯説に対する疑問は「サンタクロース巡回問題」からも示される。N人の顧客(今回の例ではN人の良い子供)が与えられたとき、サンタが計算しなければならない経路の総数は(N-1)!/2で与えられる。2で割っているのは「対称巡回サンタクロース問題(A家からB家間での距離と、B家からA家間での距離が同じという性質がある場合)」であるからだ。

　子供の家N=100までの場合の、サンタが計算しなければならない経路の総数(N-1)!/2を以下に示してみる。
 

子供の家N=100までの場合のサンタが計算しなければならない経路の総数
横軸=N、縦軸=計算しなければならない経路数

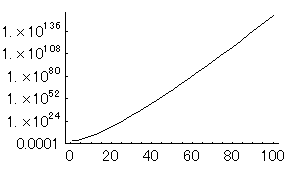　どうだろうか、Nが少し増えると爆発的にサンタが計算しなければならない経路の総数(N-1)!/2が増えていくのがわかると思う。一軒多くなるだけで、ものスゴイ数の計算をしなければならなくなるのである。サンタが実際に配達して回るのも大変だが、その前に配達経路を決める計算量は実はもっと大変なのである。

　先の人口増加の割合をこれに加えるならば、「サンタが計算しなければならない経路の総数」は天文学的数字になることは明白である。

　そこで、私はやはりサンタ複数犯説が真実に近いと思うのである。サンタ複数犯説が正しいとするならば、ッ実はこの「サンタクロース巡回問題」は遥かに容易に解くことができるようになるのである。

　それでは、複数サンタがいるときの「サンタクロース巡回問題」を考えてみよう。サンタが複数のm人いる場合を考える≠ニA「サンタが計算しなければならない経路の総数」はm*(N/m-1)!/2で示される。
　一例として、サンタが1,2,10人の場合を示してみる。
 
 

複数サンタがいるときの
子供の家N=100までの場合のサンタが計算しなければならない経路の総数
横軸=N、縦軸=計算しなければならない経路数
黒=サンタが一人
緑=サンタが二人
紫=サンタが十人

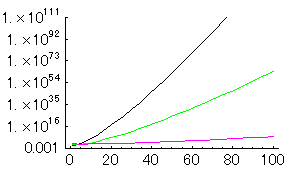　このグラフからサンタが複数いる場合と、単独の場合とで巡回経路を考える手間が全然違うのがわかるだろう。サンタが2人いると、計算量は半分になるのではなく、ものすごく少なくなるのである。

　実際の巡回においての仕事量は、サンタがm人いれば1/mになる。しかし、その前準備はサンタがm人いれば((N-1)!/2)/(m*(N/m-1)!/2)分の一になるのだ。簡単に言えば、メチャクチャ楽になるのだ。サンタが一人では事実上サンタがプレゼントを配ることは不可能だけれど、複数犯であれば容易にプレゼントを配ることができるのだ。

　このように「複数サンタクロース巡回問題」を考えることにより、サンタは複数いることが明らかだと私は思うのだ。

　ただこれだけでは、不十分だ。全世界の子供達も年を経るに従って、爆発的に増えている。サンタが複数いるにしても、それでもやはり大変だ。サンタ達の人数も爆発的に増えていかなければ、とてもじゃないがやってられないことだろう。

　それを解決する一つの答えはこうだ。「子供が増える割合に従って、サンタも増える」と考えるのだ。子供が一人増えると、サンタも一人増えるのだ。そうすれば、何の問題もない。子供が一人現れると、サンタも一人増えるのであれば何の問題もなくなる。

　ところで、「子供が一人現れると、サンタも一人増え、サンタの数が子供と同じ比率で増えていく」ということは、子供たちがいずれサンタになるという考えが自然だとは思えないだろうか。そうだ、子供達がサンタになるのだ。子供達が大人になって、そしてサンタになるのだ。

　もしかしたら、それはサンタという名前ではないのかもしれない。普段は他の名前で呼ばれているのかもしれない。けれど、クリスマスだけはサンタという名前になるのだ。電話ボックスで着替えるちょっと情けないスーパーマンのように、クリスマスイヴだけは彼らは変身するのだ。

　こうして、サンタ達は子供の枕元にやってくる。むかし子供だったサンタ達が子供達の枕元にやってくる。そして、夢を見ている子供達が起きてしまわないように、そっと枕もとにプレゼントを置く。

　サンタなんかこれまで私の枕元には来なかった、という人たちも多いのかもしれない。けれど、きっと、そんな人たちもまたサンタになっていくのだろう、そして、その時、本当にサンタがいる、ということに気づくのだろう。
 

■五反田・九段下

　五反田で技術情報協会の「デジタルハーフトーニングの最適化と評価手法」阿部氏の4時間にわたる講習の資料は255枚。FFhで「すべてがFになって」終わるという辺りが実に凝っていた。4時間の講習というような場合には、本番で初めて「最初から最後まで喋る」とならざるをえないから、結構時間調整に不安を感じたりすると思うが、その状態でFFh枚に調整できる辺りがスゴイ。

　巡回セールスマン問題の解説では借力氏の「超東京地図」が例に出されており、思わず笑ってしまった。エッシャーのDay and Nightスクリーンや純愛スクリーンや…と、とても楽しめた。気に入ったスライドの内の一枚は「最適解を探すためのやり方」を示した次のようなスライド。(ちょっと変えてあるけれど)

　　集中化と多様化・集中化　・「良い解に近いところには、良い解が存在する」　　という性質を信じ、良い解の周りで集中的に探索・多様化　・「悪い解の周りで彷徨い、良い解に出会えない」　　ことを避けるため、今までと違う場所を強制的に探索

　夜は、きっと最初で最後の武道館アリーナ最前列。アンコール最後「私が見てきた全てのこと 無駄じゃないよって君に言って欲しい」の"ハローグッバイ"まで二時間半。

■「IronRuby」+「Mathematica Player」=「∞の可能性」

　まだまだ、「(.NETで動くRubyである)IronRubyと(無料配布されている)Mathematica Playerの組み合わせ技」にハマっています。素晴らしく楽しく使うことができる言語環境Mathematicaと、やはり素晴らしく便利なRubyと、そして（多分便利な）.NETを一緒に用いることができるというのは、とてもエキサイティングな体験だからです。

　今日は、まずは「Mathematicaの使い方」を眺めながら、クラスタ分析をIronRuby+Mathematica Playerでなぞってみました。

include System
require 'Wolfram.NETLink'
include Wolfram::NETLink
kernelLink=MathLinkFactory.CreateKernelLink()
kernelLink.WaitAndDiscardAnswer()
result=kernelLink.EvaluateToOutputForm(
  'datarecords = {
{"Joe", "Smith", 158, 64.4}, 
{"Mary", "Davis", 137, 64.4}, 
{"Bob", "Lewis", 141, 62.8}, 
{"John", "Thompson", 235, 71.1},
{"Lewis", "Black", 225, 71.4}, 
{"Sally", "Jones", 168, 62.},
{"Tom", "Smith", 243, 70.9}, 
{"Jane", "Doe", 225, 71.4}};', 0)
result=kernelLink.EvaluateToOutputForm(
  'FindClusters[Drop[datarecords, None,
   {1, 2}] -> datarecords]', 0)
puts result
kernelLink.close

こうコードを書くと、各人の身長と体重のデータを用いて、それらの人を何グループかにクラスタリングを行うことが簡単にできます。たとえば、こんな結果が返ってきます。

{{{Joe, Smith, 158, 64.4}, {Mary,Davis, 137, 64.4}, {Bob, Lewis, 141, 62.8},{Sally, Jones, 168, 62.}}, {{John,Thompson, 235, 71.1}, {Lewis, Black, 225, 71.4}, {Tom, Smith, 243,70.9}, {Jane, Doe, 225, 71.4}}}

見事にクラスタリングされています。もちろん、これは、Mathematicaのマニュアルそのままのコードです。けれどそんな処理をRubyで行うことができて、その結果をRubyでさらに使うことができるのはとても便利です。

あるいは、

include System
require 'Wolfram.NETLink'
include Wolfram::NETLink
kernelLink=MathLinkFactory.CreateKernelLink()
kernelLink.WaitAndDiscardAnswer()
result=kernelLink.EvaluateToOutputForm(
  'FindShortestTour[
{{4, 3}, {1, 1}, {2, 3}, {3, -5}, 
  {-1, 2}, {3, 4}}]', 0)
puts result
kernelLink.close

なんていうコードを書けば、二次元座標群を「どうすれば最短時間（距離）で巡ることができるか？」という巡回セールスマン問題を解くことができます。もちろん、答えはすぐ返ってきて、

{11 + Sqrt[2] + Sqrt[5] + 3 Sqrt[10],
 {1, 3, 5, 2, 4, 6}}

というように、「最短距離」と「どのように点（都市）を廻れば良いか」がたちどころにわかります。

　クラスタ分析、巡回セールスマン問題・・・ありとあらゆる問題を、IronRubyとMathematica Playerのタッグは解いてくれます。「IronRuby」+「Mathematica Player」を使っていると、「∞の可能性」を実現できるような「錯覚」を覚えます