2020-08-30[n年前へ]
■市街地の高低を、アルプスをに見立てて尾根沿いに山歩き。 
大都市周辺のベットタウンの住宅地、住宅地に隠れてる山脈や渓谷を「山歩き」
 たとえば渋谷の道玄坂など、都市に「坂道」がたくさんあることでわかるように、大都市にも山や谷が残っています。それと同じように、あるいはそれ以上に、大都市の周辺に位置するベットタウンにも、山や谷があるものです。たとえば、右の画像は、標高を強調した横浜・新横浜周辺の3Dマップです。……今朝は、そんな市街地アルプスの尾根沿いに「縦断山歩き」をしてみることにしました。歩いてみたのは、新横浜近くにある「鴨居アルプス」です。
たとえば渋谷の道玄坂など、都市に「坂道」がたくさんあることでわかるように、大都市にも山や谷が残っています。それと同じように、あるいはそれ以上に、大都市の周辺に位置するベットタウンにも、山や谷があるものです。たとえば、右の画像は、標高を強調した横浜・新横浜周辺の3Dマップです。……今朝は、そんな市街地アルプスの尾根沿いに「縦断山歩き」をしてみることにしました。歩いてみたのは、新横浜近くにある「鴨居アルプス」です。
住宅トレッキングのコツは「ひたすらに高い尾根沿いを歩く」
 市街地アルプスのコツはとても簡単。少しでも標高が高そうな方向に進み、どんな路地でも交差点でも、ひたすらに標高が高そうな方向に進むだけ。つまりは、ポール・グレアムが言う「風上を目指せ」と同じルールです。そんなルールに従っていると、たとえば右の写真のように、尾根沿いの道が見えてくるのです。
市街地アルプスのコツはとても簡単。少しでも標高が高そうな方向に進み、どんな路地でも交差点でも、ひたすらに標高が高そうな方向に進むだけ。つまりは、ポール・グレアムが言う「風上を目指せ」と同じルールです。そんなルールに従っていると、たとえば右の写真のように、尾根沿いの道が見えてくるのです。
市街地アルプスから見える「大都会のビル」も格別な素晴らしさ
 ひとたび、こんな山脈縦断コースに出たら、後は自動的に興味深い色んな風景に、自動的に出会うようになります。たとえば、右の写真のように、横浜のみなとみらい……つまりはかつての未来的な風景が、ベットタウンな住宅地の隙間から見えてきたりもします。
ひとたび、こんな山脈縦断コースに出たら、後は自動的に興味深い色んな風景に、自動的に出会うようになります。たとえば、右の写真のように、横浜のみなとみらい……つまりはかつての未来的な風景が、ベットタウンな住宅地の隙間から見えてきたりもします。
 あるいは、路地を少し歩くだけで、反対側の住宅地の向こうに東京都心の高層ビル街が見えてきたりもするのです。今年、オリンピックがあるはずだった2020年のTOKYOが、少し寂しい色合いにも見えたりして、そんな景色を見ることができるのも、市街地アルプス山歩きの楽しい利点のひとつです。
あるいは、路地を少し歩くだけで、反対側の住宅地の向こうに東京都心の高層ビル街が見えてきたりもするのです。今年、オリンピックがあるはずだった2020年のTOKYOが、少し寂しい色合いにも見えたりして、そんな景色を見ることができるのも、市街地アルプス山歩きの楽しい利点のひとつです。
尾根近くの谷には、不思議な秘境があったりも

 市街地に位置するアルプスでも、少し尾根を離れるだけで、秘境的な不思議な場所が隠れていたりもします。たとえば、右の画像は、鴨居アルプスの尾根沿いに隠れていた、そんな奇妙な空間です。どうすれば辿り着くことができるかわからないような場所に、不思議な神社が隠れていたりもするのです。
市街地に位置するアルプスでも、少し尾根を離れるだけで、秘境的な不思議な場所が隠れていたりもします。たとえば、右の画像は、鴨居アルプスの尾根沿いに隠れていた、そんな奇妙な空間です。どうすれば辿り着くことができるかわからないような場所に、不思議な神社が隠れていたりもするのです。
自分が好きに決めた場所、そこが市街地アルプスの山頂という名のゴール地点
 市街地アルプスの山頂は、自分が好きに決めれば良いものです。「ここが山頂と決めた」と自分が思った瞬間に、そこが市街地アルプスの縦断山歩きのゴール地点になります。……もちろん、その次の瞬間に「いや、あの先にある交差点を山頂にしよう!」と思ったならば、次の山頂ゴールはその場所に移動します。右の写真は、今朝の縦断山歩きで自分で決めた、鴨居アルプスの山頂です。
市街地アルプスの山頂は、自分が好きに決めれば良いものです。「ここが山頂と決めた」と自分が思った瞬間に、そこが市街地アルプスの縦断山歩きのゴール地点になります。……もちろん、その次の瞬間に「いや、あの先にある交差点を山頂にしよう!」と思ったならば、次の山頂ゴールはその場所に移動します。右の写真は、今朝の縦断山歩きで自分で決めた、鴨居アルプスの山頂です。
住宅地にある市街地アルプスを歩くのは、意外に楽しく新鮮なのかも、と思います。
2020-02-18[n年前へ]
■ソフトの力で、すべての人に「音を楽しむ可能性」を作り出せ! 
 「ソフトウェアデザイン 2020年3月号」に記事を書きました。Pythonでシンセサイザーを作り、さらに、ギター・ボーカル用エフェクターや、100円でベースギターを自作したり、ボコーダーを作ってみる話です。
「ソフトウェアデザイン 2020年3月号」に記事を書きました。Pythonでシンセサイザーを作り、さらに、ギター・ボーカル用エフェクターや、100円でベースギターを自作したり、ボコーダーを作ってみる話です。
先月初旬、タイの「こどもの日」をバンコクで眺めながら、その日の夜から次の日の早朝にかけて、楽しく書いてみた記事です。


2020-01-25[n年前へ]
■女性芸能人の法則「”8″が付いてるスリーサイズはかなりウソ!?」…を誰でも読むことができるようにしました。 
Software Design 2019年12月号『芸能人の嘘と真実!?ー「身長・ 体重」徹底大調査!?』の番外編、『女性芸能人の法則「”8″が付いてるスリーサイズはかなりウソ!?」』も、誰でも読むことができるようにしました。
2020-01-24[n年前へ]
■『ステレオ撮影で切り取った「立体・質感情報」を、ブラウザやThe Looking Glassで リアルに豊かに表示する!』を誰でも読めるようにしました。 
(普通基準を見失っていた)ソフトウェアデザイン'19年7月号『ステレオ撮影カメラで 「立体的で質感豊かな世界」を記録する!』…のさらに冷静さ無い続編『ステレオ撮影で切り取った「立体・質感情報」を、ブラウザやThe Looking Glassで リアルに豊かに表示する!』を誰でも読めるようにしました。
2020-01-23[n年前へ]
■Wat Paknam Bhasicharoen(ワット・パクナム・パーシーチャルン)で撮影した3Dスマホ映像とか 
「(タイの)こどもの日」「Maker Faire Bangkok」「(中国旧正月の)春節のバンコク中華街」が時期的に密集していたので、タイ・バンコクに行ってみました(一月少し前も行っていた気がしますが)。

 インスタ映えするということで(日本人観光客が多く訪れ・とても悪評を拡げているという)Wat Paknam Bhasicharoen(ワット・パクナム・パーシーチャルン)にも、早朝8時に行ってみました。日本人的にインスタ大人気の最上階も面白かったのですが、そこに辿り着くまでの途中階も、…ガラクタ市で「何かの古道具」探す一人として、とても楽しめました。どういうことかというと、さまざまな過去の歴史上で作られた技術展示や、(仏教系の新興宗教にまつわる)日本訪問の記録や、そして「(ガラスや宝石を使った)透明球体」展示がされていたからです。
インスタ映えするということで(日本人観光客が多く訪れ・とても悪評を拡げているという)Wat Paknam Bhasicharoen(ワット・パクナム・パーシーチャルン)にも、早朝8時に行ってみました。日本人的にインスタ大人気の最上階も面白かったのですが、そこに辿り着くまでの途中階も、…ガラクタ市で「何かの古道具」探す一人として、とても楽しめました。どういうことかというと、さまざまな過去の歴史上で作られた技術展示や、(仏教系の新興宗教にまつわる)日本訪問の記録や、そして「(ガラスや宝石を使った)透明球体」展示がされていたからです。

散歩中に眺めたものは、いつでも複数視点からの立体映像を残すようにしています。…というわけで、下に貼り付けたのはWat Paknam Bhasicharoen(ワット・パクナム・パーシーチャルン)でスマホ撮影した立体動画からのワンショット、です。眺め方は、平行法になります。

2020-01-22[n年前へ]
■「エクセルの計算順序」から「コンピュータの歴史」を感じよう! 
4月中旬発売のソフトウェアデザインで連載最終回になるので、「幻の第一回ボツネタ」を読めるようにしてみました(読みやすい形でのアップロードはまた別にやっておこうと思います)。
「エクセルの計算順序」から「コンピュータの歴史」を感じよう!
■「エクセルの計算順序」から「コンピュータの歴史」を感じよう! 
-2020年になった今、1950-1980の時代を振り返る-
-1^2の計算結果は-1になる!?「エクセルの計算順序」の謎
オフィス作業の多くがMicrosoft Excel(エクセル)上で行うのが当たり前となっています。そのエクセルでシートを開き、”= 0 - 1^2”, “= -1^2 + 0”という2式をセルに入力すると、どんな計算結果が出力されるでしょうか?
「どちらも-1になるはず」と答える人が多いかもしれませんが、実際に式をセルに入力すると、”=0 - 1^2→ -1”, “=-1^2+0→1”という結果になります(図1(a))。だからといって、「エクセルの計算バグ!?」と考えてはいけません。なぜなら、これは伝統正しいエクセルの仕様だからです。

同じ“-”でも二項演算子の”-”と単項演算子の”-”がある?
「どちらも-1になるはず」という答は、2式をそれぞれ0 –(1^2)と-(1^2)+0という順番に暗算から得られたはずです。…けれど、エクセルが行う計算順は、それとは違う0 –( 1^2)と(-1)^2+0という順番です。その結果、 -1と1という計算結果をエクセルは得るのです。
「減算よりべき乗の演算の方が優先されるべきだから、エクセルの計算順はやはりおかしくない?」と思う人もいるかもしれません。しかし、エクセルも、2つの値間でべき乗計算を行う”^”は、減算を行う“-”より優先する仕様になっています。
この2式には、”-” ”^” ”+”という演算子が登場します。そのうちの、”^”と”+”についてはすべて、左右の2値を使い演算を行う2項演算子です。ところが、”-”については、”= 0 - 1^2”では(被演算子が左右にある)2項演算子ですが、“= -1^2 + 0”については、(被演算子が左右の片方にしかない)演算で使う値が一個の単項演算子(Unary operator)として、エクセルの計算が行われます(図1(b))。
“= -1^2 + 0”の”-”は、”-”の右側にある1を符号反転させる演算子で、エクセルが採用する演算子優先順では、単項演算子は二項演算子に優先します(図1(c))。その結果として、-1^2+0は (-1)^2+0 として計算されて、1という値が出力されるのです。
コンピュータを広めた表計算ソフトが生まれた時代の計算順を調査しよう!
エクセルの演算順序が、一般的な代数式の計算順序と異なる仕様になった理由はわかりません。「エクセルが開発された当時、標準的に使われていたLotus 1-2-3との互換性を考えたのではないか?」とも思いたくなりますが、そうでもありません。
なぜなら、Lotus 1-2-3では、エクセルと異なる-1^2=1という計算結果になるからです。また、1985年発売のエクセルの開発チームは、Lotus 1-2-3(1983年発売) に先行して1982年発売のMultiPlanも開発しましたが、Multiplanでもやはり-1^2=-1と計算していたからです。
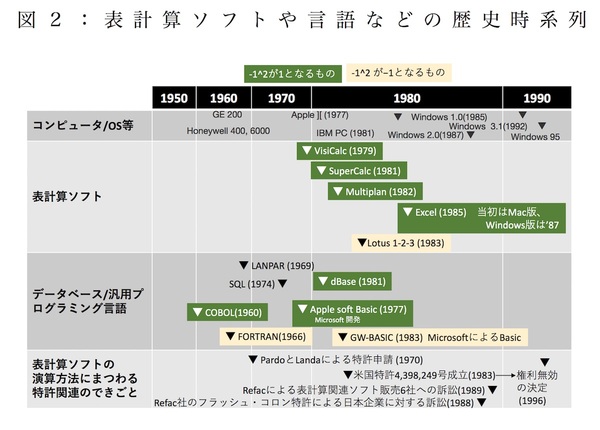
エクセルやMultiplanが発売当時を調べてみると、面白いことがわかります。表計算ソフトという形態を作り出したVisiCalcも、当時の表計算ソフトの用途と重なるところも多かったデータベースソフトdBaseでも、ビジネスプログラミング言語のCOBOLも、多くのソフトでエクセルと同じ演算結果を出力します(図2、図3)。 そんな時代背景を踏まえれば、エクセルが「単項演算子―は2項演算子^に優先する」という仕様にしたということも、いたって自然にも思えてきます。

セル間の計算順序には「2つの方法」が使われている
「セル間の演算を簡単にできる」のが、今ではエクセルに代表される表計算ソフトウェアです。だから、エクセル等が計算を行う際には、セル内の演算順だけでなく、セル間の計算順序もきちんと決まっていて、エクセルでは、2つの異なるセル間の計算方法が使われています。
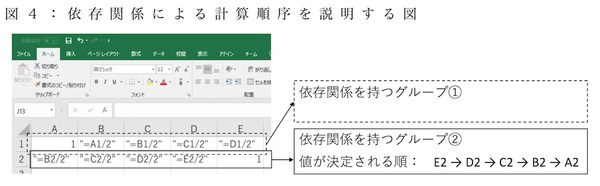
「依存関係ごとに、値が定まるものから先に」の計算順
通常使われているセル間の計算順は、「セル間の依存関係を(ツリー構造で)辿り、値が定まっている“源流“から計算を順に行っていく」というものです。たとえば、セルB2に”=10-B3”、そしてセルB3に”6”という文字が入力されていたら、まずは「セルB2の前に、セルB3を定義する」という依存関係を持つグループの中で順番を生成した上で、セルB3を表す変数に値6を設定し、そしてB3で10-6という演算を行って、結果の4を格納するのです。もしも、ユーザーがどこかのセルを書き換えた時には、そのセルが属する依存関係のグループ内のみで、上流から下流に向かって計算が行われます。
アルファベット順+Zの法則(左→右、上→下)の計算順
もうひとつのセル間計算順は、「通常の方法が使えない場合」に使われます。具体的には、自己参照(循環参照)が行われている場合、言い換えれば「依存関係を辿っていくと、いつの間にか自分に辿り着いてしまい、無限ループに陥る場合」に使われます。計算をするのに、自分(自セル)自身の値を入力(右辺値)として使う状況があるの?と感じられるかもしれません。けれど、方程式を解く必要がある場合など、自己を参照するような数式に対する計算ができると便利なことも多いのです。
たとえば、x ==(2 -3 y) / 4, y == (5 – 6 x) / 7という一次連立方程式を解きたい場合、セルB1とB2をxと yだとした上で、それぞれに =(2 -3*B2)/4と =(5 - 6*B1)/7という式を入れてみます。すると、「循環参照が行われています・・・」という警告が出るので、設定を「反復計算を使う(計算回数はとりあえず100)」と変えて、反復計算を実行させる(F9を押す)と、x(B1)=-0.1, y(B2)=0.8と連立方程式の計算結果が求まります。
反復計算を行う場合には、循環参照が行われている部分に対し、アルファベット順で前方のシートから、そして同じシート内では左から右へ・上から下への順で(A1からA行を左から右へ、次はB行を左から右へ…と)計算が行われます。そして、最大反復回数に達するか、各セルでの計算結果の変化値が所定の値を下回るまで、この計算が繰り返されるのです。
循環参照による反復計算は、普通とは言えないかもしれません。とはいえ、方程式を解いたりする場合などには必須になることも多い計算手法です(*この方法では、必ずしも計算が収束するわけではありません)。
表計算ソフトが生まれた頃は、反復計算方式が使われていた
表計算ソフトが登場したての’80前半、すべての表計算ソフトが、どのような計算であっても、反復計算方式を使っていました。もう少し正確に言えば、シートに含まれるセルに対して(Zの法則など)所定の順番で計算を行い、値が変わらなくなるまでユーザが手動で計算を繰り返していました。
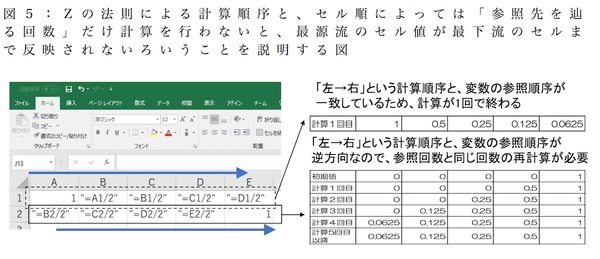
「値が変わらなくなるまで再計算を行う」必要がなぜあるかというと、他のセルを参照する計算式が使われている場合、セルの並び順によっては「参照先を辿る回数」の再計算を行わなければ、最源流のセル値が最下流のセルまで反映されないからです(図4)。そのため、初期の表計算ソフトを使う際には、セルの値を見ながらユーザが計算を繰り返さなければならなかったのです(図5)。
最源流のセルから下流へと「依存関係に沿って計算していく方式」が一般的に用いられるようになってから、各セルに対し1回の計算だけで結果が得られるという、現在の表計算ソフトの形態に落ち着いたのです。
表計算の計算方法を提案する「幻の基本特許」が存在していたが…
「依存関係を踏まえ、上流セルから計算を行う」という表計算ソフトの土台ともなっている演算手法ですが、実は「幻の基本特許」があります。
今の表計算ソフトの原型となったVisiCalcが登場する1979年より10年も前の1969年、LANPARというデータ操作言語が米国人Rene PardoとRemy Landaにより開発されます。LANPARが採用した変数間の演算順序は、automatic forward referencing (natural order calculation)と呼ばれ、「値が定義されているものから先に計算を行う」という表計算の計算順序に関する基本アルゴリズムと言えるものでした。
申請から13年を経て成立した特許で、さらに6年後に訴訟開始
PardoとLandaは、1970年に計算手法に関する特許申請を行いましたが、「技術の内容説明が不足」という理由で申請は却下されます。しかし、彼らは特許成立に向けた活動を続け、「プログラミングに関わる一般知識を持つ通常の人であれば、特許で公開された内容から技術を再現できる」とする一般の3名のプログラミング経験者による宣誓書を提出することで、特許申請から13年を経た1983年、米国特許4,398,249号としてようやく認めさせます(図6)。
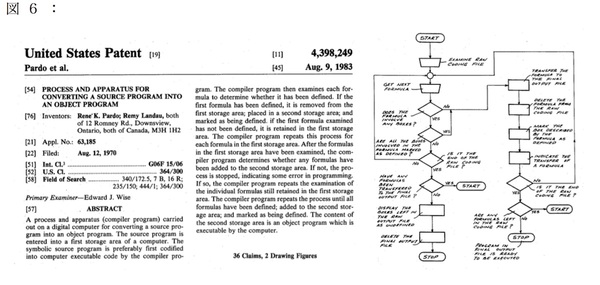
そして、すでに表計算ソフトが必需品となっていた1989年、Pardoらは、「1ヶ月以内に少なくとも2名の特許侵害者を訴える」という条件付きで、パテント・トロール企業として有名なRefacに特許権利の5%を譲渡します。Refacは、デジタル時計の表示に関する特許、「時と分表示の間にあるコロンを点滅させる」というフラッシュ・コロン特許で、日本企業を中心に100億円以上の特許使用料を得た企業です。
そんな経緯を受けて、Refacは表計算ソフトを販売していた6社、Lotus(Lotus 1-2-3), Microsoft(Excel), Borland(Quattro), Ashton-Tate(Full Impact), Computer Associates(SuperCalc), Informix(Wingz)に対して、膨大な特許使用料を請求する訴訟を起こします。権利期間17年にわたる特許使用料として、膨大な金額を請求する訴訟です。
「特許内容は十分」と宣誓したプログラミング経験者、実は…
「表計算ソフトの基本特許は、膨大な特許使用料を生み出した」という結末を迎えたかというと…そうではありませんでした。その訴訟の結果は「大どんでん返し」で終わります。
1989年に始まる審判で、「Pardoらの特許申請には不正があり、権利無効である」とLotusが主張したのです。どういうことかというと、「特許内容は十分詳細である」と証言したプログラミング経験者というのが、実はLANPERの開発経験を持つ関係者で、その事実を特許商標局に対して隠していたというのです。「特許申請に対して全く前提知識を持たない人であっても、技術内容を理解できる」という意見を述べる宣誓であるはずが、実はそうではないものを提出していたことを「不正」と判断されたのです。そして、1996年、表計算ソフトの演算手法に関する基本特許とも言える米国特許4,398,249号は、「権利を行使できない幻の特許」と決定されたのでした。
表計算ソフトの演算順…そこには「面白い歴史」が詰まってた
個人でコンピュータを使えるようになった20世紀の後半も、あるいはPCがあたりまえの道具になった21世紀の今現在も、その価値や原動力となっているのが表計算ソフトです。そんな表計算ソフトの演算(計算)順を今回は調査してみました。意外なほど、たくさんのエッセンス、とても興味深いコンピュータの歴史がそこには詰まっていました。
2020-01-18[n年前へ]
■右肩下がり時代の秘株式投資術! ~東証株解析で資産約6万倍!?~ 
 1月18日発売のソフトウェアデザイン 2020年2月号に、『右肩下がり時代の秘株式投資術! ~東証株解析で資産約6万倍!?~』を書きました。4月発売の5月号が連載最終回なので、「最終回の4回前」の記事になります。記事を書いたのは、2019年、令和元年の11月の頃のバンコクでした。「Python Pandasを使うと何ができるか」を、相鉄線のCMを聴きながら書いてみた記事です。
1月18日発売のソフトウェアデザイン 2020年2月号に、『右肩下がり時代の秘株式投資術! ~東証株解析で資産約6万倍!?~』を書きました。4月発売の5月号が連載最終回なので、「最終回の4回前」の記事になります。記事を書いたのは、2019年、令和元年の11月の頃のバンコクでした。「Python Pandasを使うと何ができるか」を、相鉄線のCMを聴きながら書いてみた記事です。
 書いたのは「経済が右肩下がりで縮小していくような時代と場所で、それでもお財布の中身を(株に頼って)増やす方法」を、わずか4ページで考え・実装してみた記事です。…そんな方法あるわけない!とか他のやり方をした方が良い!と感じたりもしますが…記事書きと同じアルゴリズムで、4ヶ月ほどの株売買をしてみた結果、年利にして9パーセントのプラスとなったので、完全に無根拠な記事ではないかもしれません。
書いたのは「経済が右肩下がりで縮小していくような時代と場所で、それでもお財布の中身を(株に頼って)増やす方法」を、わずか4ページで考え・実装してみた記事です。…そんな方法あるわけない!とか他のやり方をした方が良い!と感じたりもしますが…記事書きと同じアルゴリズムで、4ヶ月ほどの株売買をしてみた結果、年利にして9パーセントのプラスとなったので、完全に無根拠な記事ではないかもしれません。
 記事の中に、たとえば(小さく配置された)図3とか図7の株価グラフの中に、30年間くらいの色んな企業の毎日が詰まっています。だから、そのグラフに書かれた社名の中の人たちには、少し面白いかも、と思います。昭和・平成・令和を生きてる世代には、色んな意味で絶対面白いはずの記事になります。
記事の中に、たとえば(小さく配置された)図3とか図7の株価グラフの中に、30年間くらいの色んな企業の毎日が詰まっています。だから、そのグラフに書かれた社名の中の人たちには、少し面白いかも、と思います。昭和・平成・令和を生きてる世代には、色んな意味で絶対面白いはずの記事になります。
2019-12-18[n年前へ]
■銀塩写真をスマホで再現!?…一番大好きな思い出は、一番似合うフィルムの色で染めてやる。 
 大瀧詠一「君は天然色」や、ポール・サイモン「僕のコダクローム」を聴きながら書いた記事が、12月18日発売のソフトウェアデザイン 2020年1月号に掲載されています。題して、「銀塩写真をスマホで再現 !?......一番大好きな思い出は、一番 似合うフィルムの色で染めてやる」です。もしも、「切なく懐かしく思い出す風景があったなら、そんな景色には「一体どんなフィルムの色調・階調が似合うだろう? 」と考えながら、書いた記事です。
大瀧詠一「君は天然色」や、ポール・サイモン「僕のコダクローム」を聴きながら書いた記事が、12月18日発売のソフトウェアデザイン 2020年1月号に掲載されています。題して、「銀塩写真をスマホで再現 !?......一番大好きな思い出は、一番 似合うフィルムの色で染めてやる」です。もしも、「切なく懐かしく思い出す風景があったなら、そんな景色には「一体どんなフィルムの色調・階調が似合うだろう? 」と考えながら、書いた記事です。
11月の満月の夜、東南アジアで灯籠流しを眺めたり、日本に戻り通夜に行ったり、連れ合いを亡くした人がいたり…そんな逆戻りできない時の流れを眺めながら、二度と戻らないそんな景色を、いつか誰もが見送る時を考えながら、Pythonコードとその説明記事を書いたものです。
2019-10-18[n年前へ]
■泡が下降を続ける!?--ギネスカスケードの謎を解け! 
「ソフトウェアデザイン 2019年11月号」に『泡が下降を続ける!?--ギネス/カスケードの謎を解け!』を書きました。いわゆるひとつの、近赤外線撮影と速度場抽出のPythonコードによる流体解析の話です。
2019-09-24[n年前へ]
■太田市パチンコ店女児連れ去り事件(ゆかりちゃん事件)の容疑者ビデオをTecoGANで高解像度化してみる 
「北関東連続幼女誘拐殺人事件(足利事件はその一部)」の一部とも言われる「太田市パチンコ店女児連れ去り事件(ゆかりちゃん事件)」、ビデオ超解像技術であるTecoGANを使い、その容疑者ビデオを高解像度化してみた。上が元画像で下が高解像度化したもの。
2019-09-17[n年前へ]
■手回し計算器でGoogleと大決闘!目指せ円周率……全3桁 
 「ソフトウェアデザイン 2019年10月」に『手回し計算器でGoogleと大決闘!目指せ円周率……全3桁』を書きました。円周率をウォリス(Wallis)の公式を使って、手回し計算器の(履歴保持機能を使い)乗算積で計算していく話です。
「ソフトウェアデザイン 2019年10月」に『手回し計算器でGoogleと大決闘!目指せ円周率……全3桁』を書きました。円周率をウォリス(Wallis)の公式を使って、手回し計算器の(履歴保持機能を使い)乗算積で計算していく話です。
そしてまた、手回し計算器が使われていた'50年代の話だけでなく、その後後の'70〜'80、そして、'90移行の今にいたる計算器の話です。
2019-09-16[n年前へ]
■かまいたちの机上の空論城 
関西テレビの「かまいたちの机上の空論城」という番組のお手伝いをした。輪ゴムでバンジージャンプに挑戦という実験のサポートをしたのだけれど、通常限られる日程や安全性確保問題を、色々な工夫で「クリア」したことが、面白かった。
収録現場で眺めた「高いところからボールを投げ下ろすと、時速150kmを超えるか?」という実験は、直感的に層流条件での終端速度からの逆計算をすると、野球硬球条件だと150km/hに達するのは不可能になる気がした。…といっても、ナックルボールの流体解析などで見るように、野球ボールのピッチングは、層流・乱流混在条件だから、もう少し現実的に考えると、典型的な投手の初速・終速測定結果から、「150km/hあたりの空気抵抗による加速(減速)度」を見積もると、およそ10m/s^2。…これは、重力加速度をうわ待っているから、やはり、絶妙に「どんなに高いところからボールを投げても、ボール速度は150km/hには達しないかも」と、収録現場で考えたりした。
2019-08-13[n年前へ]
■プレート境界で揺れ動く!日本列島の動きを可視化せよ! 
 ソフトウェアデザイン 2019年9月号に『プレート境界で揺れ動く!日本列島の動きを可視化せよ!』を書きました。測地データをダウンロードした上で、Python / Jupyterを使い、変位解析・簡易歪み解析をとても簡単に遊んでみたりする記事です。
ソフトウェアデザイン 2019年9月号に『プレート境界で揺れ動く!日本列島の動きを可視化せよ!』を書きました。測地データをダウンロードした上で、Python / Jupyterを使い、変位解析・簡易歪み解析をとても簡単に遊んでみたりする記事です。
日本列島近くの地震発生分布や地殻変動の変位分布、あるいは、地殻変動から推定される歪み分布…そんなものを眺めてみると、色んな解析をしてみたくなるはずです。
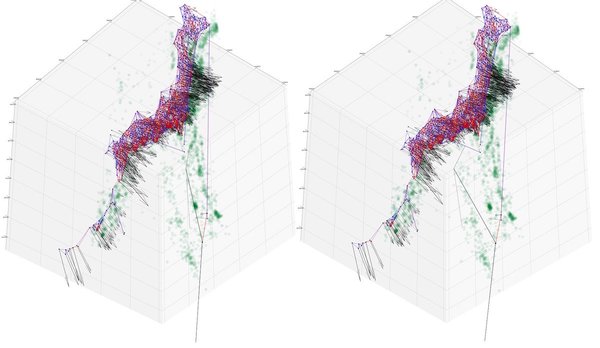
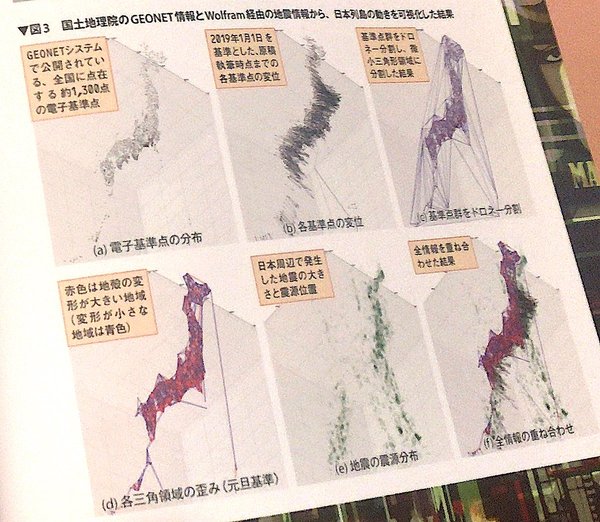 たとえば、右にあるのは、そんな解析を行った結果の数例。こんな日本列島が刻々と形を変えるさまを眺めてみると、きっと、地震予知とかそんな無理目の挑戦をしたくなる人も多いかもしれません。
たとえば、右にあるのは、そんな解析を行った結果の数例。こんな日本列島が刻々と形を変えるさまを眺めてみると、きっと、地震予知とかそんな無理目の挑戦をしたくなる人も多いかもしれません。
また、記事中の解説コードや処理はすべてフル3Dです。つまり、たとえば、The Looking Glass をお持ちなら、日本の地殻変動をリアルに立体的に眺めることができる…ということになります。プレート境界で揺れ動く日本列島の動きを、立体的に眺めてみるのも面白いのではないでしょうか。
2019-07-19[n年前へ]
■1.5億キロメートル先で輝く太陽、表面温度を計りたい!「スマホで作る2次元分光カメラ」 
ソフトウェアデザイン 2019年8月号に『1.5億キロメートル先で輝く太陽、表面温度を計りたい!「スマホで作る2次元分光カメラ」』を書きました。二ヶ月前原稿は『秒速340メートルで進む音、ステレオ音声動画の「音源方向」を可視化する!』というタイトルで、1ヶ月前に書いた原稿は、『秒速30万キロメートルの光と影、ステレオ撮影カメラで「立体的で質感豊かな世界」を記録する!』
…つまりは、「秒速5センチメートル」とかを眺めつつ、秒速340メートルとか、秒速30万kmなエトセトラに関する記事を書いてみました。
2019-06-23[n年前へ]
■2012年公開の「メン・イン・ブラック3」にハマるの巻 
7年前に公開の「Men in Black 3」を、金曜ロードSHOW!で観たことをきっかけに、気になった箇所を知りたくて、ノーカット版で観直した。…すると、その台詞回しに感動して、思わずメモをとってしまった。
まず、10:30辺りから始終繰り返される(このエピソードに至るまでのコンテキストと矛盾せず・むしろその説明を与えてくれる)リフレイン。「過去の何が、今の現在を作ったか。なぜ、そういう現在に至ったか。」というのが、この映画のテーマだ。
How did you get to be like you? Something happened, K. What happened?あと、もうひとつ。これも、何度も出てくるリフレインだ。非常に似たフレーズで、"truth or lies?"というフレーズも、何度も出てくる。それらのフレーズは、このエピソードに至るまでのコンテキストに対して、納得感与える理由の説明を与えてくれる。過去や現在を作る、そこに至る行動に迷う理由を与えてくれる。
I don't ask questions that I don't want to know the answer to.
ちなみに、タイムトラベルもので、気に掛かる「タイムパラドクス」…それの懸念に答えるフレーズが、35:20のこれだろう。
Oh, wait. How come I remember K, but nobody else does? That means you were there! I was there?このフレーズは、プロット的に実に「上手い」ように思う。つまり、世界線は結局のところ変わっていなかったし、だから、その世界で生きる登場人物の今の行動を作り出していたのだろう…と感じさせてもくれる。
もうひとつ、忘れられないフレーズが、付け足しのように言う”You and your partner.”という台詞だ。この言葉で、主人公のうちの1人に重きをおいた"you"だとわかるので、その前に眺めた映像が「地球が破滅するシーン」ではなく、(別脚本では)it was my son. All grown up.と書かれた内容であることが、自然にわかる。
What did Griff show you back there? How important you are. You and your partner.
JAY: Can I ask you -- what did the Lama(Griffin) show you in there that made you help us? Was it the Earth being destroyed? COLONEL: No -- it was my son. All grown up. As a matter of fact, I'm late to see him -- I promised I'd watch the launch with him. JAY: Oh. Thanks. He's a lucky kid. COLONEL I'm a lucky dad. Take care. (Jayが差し出した手に握り、そして、 COLONELはJayを抱きしめる)
映画館を出るときに、絶対気持ち良くなるはずのフレーズが1:24:00の”Anything's possible"だ。ありふれて・使い古されたフレーズだけれど、過去や現在は変えられないけれど、未来だけは未だ可能性が限定されていないという、こういうフレーズは大好きだ。
結局のところ、数限りない可能性の中から、迷いの末に選べなかった選択肢を取り除いたものが、今この瞬間を作っているのだろう。
…7年前に公開の映画を観て、とても興味深かったので、思わずメモしてしまった。
2019-05-10[n年前へ]
■秒速約340m、ステレオ音声動画の「音源方向」を可視化する! 
 来週発売の「ソフトウェアデザイン 2019年6月号」に「秒速約340mで走る音を映し出すカメラ」を作るための技術入門・製作記事(4ページ)を書きました。いつか、街中で写したカメラ映像音声から、誰かの口が何かをかすかにささやく姿を眺めたい…何かが振動することで生まれた音が走る姿を眺めたい…、そんなことをいつかどこかで願ったことがある方は、少しだけでも楽しんで頂ければ幸いです。
来週発売の「ソフトウェアデザイン 2019年6月号」に「秒速約340mで走る音を映し出すカメラ」を作るための技術入門・製作記事(4ページ)を書きました。いつか、街中で写したカメラ映像音声から、誰かの口が何かをかすかにささやく姿を眺めたい…何かが振動することで生まれた音が走る姿を眺めたい…、そんなことをいつかどこかで願ったことがある方は、少しだけでも楽しんで頂ければ幸いです。
「ねえ、秒速5センチなんだって」 「桜の花びらの落ちるスピードだよ」 「秒速5センチメートル」 「秒速5センチメートル」…空間を動くものすべて、映し出して、その美しさを眺めてみたいかも。
2019-04-30[n年前へ]
■「平成」の終わり、今日も前を向いて未来へと進む。 
GW進行の3週間前、ソフトウェアデザイン2019年6月号向けに4ページ記事を書いた。校正時、タイトル冒頭に「秒速 340 メートル、」を付け忘れてしまったことに、「平成」最後の今日4月30日に気づいた。令和が始まる最初の月、5月に発売される該当記事の内容は、秒速30万キロメートルで進む光と、秒速340メートルで進む何か…にまつわる可視化記事だ。
「平成」が始まったのは、京都の吉田寮あたりをウロウロしていた頃だった気がする。そんな元号が今日終わる。時間は秒速1秒で進み、その進行方向を人は未来と呼ぶ。そして、過去を後ろにいつも振り返りつつ、今日も前を向いて未来へと進む。
2019-04-18[n年前へ]
■歴史と科学の受けと攻め。『織田信長の長槍』で風船を突ける? 
4月18日(木曜日)、 時間は23時22分~24時22分、ABCテレビ「ナイトinナイト枠(木曜日)」の「ビーバップ!ハイヒール」で、『織田信長の長槍』で風船を突ける?日本史を科学的に検証!と題して、昨年集英社から出版した『信長もビックリ!? 科学でツッコむ日本の歴史』が放映されました。
歴史と科学を掛け合わせた内容です。つまりは、歴史と科学の受けと攻め。世の中にある多くの演算は、単純な掛け算と違って、演算の順番次第で内容が変わる気がします。歴史と科学では、一体どちらが前者でどちらが後者かはわかりません。
何はともあれ、動画で解説する「歴史×科学」は意外に相性良いのかも、と思わされました。…というか、わかりやすく説明しようとした時には、適切に作成された動画解説がわかりやすいのは当然なのかも、と思わされました。
2019-04-17[n年前へ]
■100円程度の小さな工夫,スマホセンサをこんな活用するなんて! 
4月18日発売の「ソフトウェアデザイン(Software Design) 2019年5月号」に 『100円程度の小さな工夫,スマホセンサをこんな活用するなんて!』を書きました。スマホが持つセンサや入出力端子を、少し使い方を変えたりすることで、AR可視化機能を拡張してみよう!という話です。
東京の山近く、東青梅に位置する「夢の図書館」「マイコン博物館」で「コンピュータの歴史を学ぶセミナー」に参加した後、そこで(コンピュータの歴史に詳しい人に)相談した後に秋月電子に行って部品を買い、NeXTコンピュータの開発をしていた人などに(JUNETとfjの話題を振り返りつつ)回路の相談をしつつ、そんなこんなが反映されているような(反映されていないような)そんな感じのスマホ電子工作記事になります。
2019-04-16[n年前へ]
■2019年4月、京華旅社から眺めるタイ旧正月 
ベトナム航空が、ベトナム経由のバンコク往復2万5千円航空券を売っていた。そこで迷わず、発券し、タイ旧正月のソンクラーンを眺めに行った。宿は、京華旅社。楽宮旅社、ジュライホテル、台北旅社、そして京華旅社(クルンカセム・ シークルン)…つまりは、20世紀のバックパッカーの定番のうち、今も残っている最後のひとつ。
バンコクのいわゆる中央駅、フワランポーン駅横に位置する京華旅社。今の朝食は、バイキング形式で美味しい。それに、中華街とか新旧電脳街にも近い。そして、その屋上階から眺める景色はとても心地良い。すべて、何だか快適で良い。



























